Eigentlich ist der Begriff selbsterklärend. Spielt man die Töne eines Dreiklangs in umgekehrter Reihenfolge, so handelt es sich um eine Dreiklangsumkehrung. (Aha ;-)

Betrachten wir einen alten Bekannten, den C-Dur Dreiklang:

Bei der ersten Umkehrung wird der unterste Ton (der Grundton C) oktaviert, d. h. eine Oktave höher gespielt. Der Charakter des Akkords bleibt erhalten. Es ist eindeutig noch ein C-Dur Dreiklang. Das solltest Du an deinem Instrument mal ausprobieren.

Bei der zweiten Umkehrung wird wiederum der unterste Ton (jetzt die Terz E) oktaviert. Wieder ist der Akkord eindeutig als C-Dur Dreiklang zu erkennen.

Kehren wir den Dreiklang ein drittes Mal um, also das G oktavieren, so erhalten wir wieder den Ausgangsakkord eine Oktave höher.

Um die Dreiklangsumkehrungen genau zu bezeichnen gibt es verschiedene Möglichkeiten. Am gebräuchlichsten (und am einfachsten) ist die Bezeichnung nach der Umkehrung:

• C-Dur Dreiklang in der Grundstellung
• C-Dur Dreiklang in der ersten Umkehrung
• C-Dur Dreiklang in der zweiten Umkehrung

Alternativ werden Dreiklangsumkehrungen anhand Ihrer Lage bezeichnet. Die Lage richtet sich immer nach dem höchsten Ton im Akkord. In der Grundstellung ist der höchste Ton G. Dies ist die Quinte des Akkords, deswegen sagt man Quintlage. Bei der ersten Umkehrung ist C der höchste Ton. Also die Oktave zum (eigentlichen) Grundton, deshalb Oktavlage. Genauso bei der zweiten Umkehrung, E ist die Terz, also Terzlage.

• C-Dur Dreiklang in der Quintlage (Grundstellung)
• C-Dur Dreiklang in der Oktavlage (1. Umkehrung)
• C-Dur Dreiklang in der Terzlage (2. Umkehrung)

Meint man die Grundstellung oder Quintlage, so reicht es auch C-Dur Dreiklang zu sagen.

Eher selten werden die Umkehrungen auch als Sextakkord oder Quartsextakkord bezeichnet. Die erste Umkehrung nennt man Sextakkord, weil das Rahmenintervall immer eine Sexte ist (bei Dur eine kleine Sexte, bei Moll eine große). Die zweite Umkehrung nennt man Quartsextakkord, weil das Intervall vom tiefsten zum mittleren Ton eine Quarte ist und das Rahmenintervall wiederum eine Sexte ist.

Nun werden wir die Umkehrungen auf die vier uns bekannten Dreiklangtypen anwenden:

Moll:

Natürlich läßt sich ein Moll-Dreiklang genauso umkehren. Auch er bleibt immer eindeutig als Moll-Dreiklang hörbar.

vermindert:

Die Umkehrungen des verminderten Dreiklangs unterscheiden sich klanglich nicht so stark wie ihre Dur- und Moll-Kollegen.

übermäßig:

Die Umkehrungen des übermäßigen Dreiklangs stellen eine Besonderheit dar, sie sind nicht erhörbar. Bei jeder Umkehrung ergibt sich durch enharmonische Verwechslung eines Tones wieder ein neuer übermäßiger Dreiklang, wenn man wieder vom tiefsten Ton des Akkordes ausgeht. Hört man einen übermäßigen Dreiklang, so identifiziert unser Ohr am ehesten den tiefsten Ton als Grundton. Es ist also nicht möglich eine Umkehrung eines übermäßigen Dreiklangs zu hören.

Dem aufmerksamen Betrachter wird aufgefallen sein, daß im obigen Notenbeispiel der E+ Dreiklang eigentlich aus den Tönen E, Gis und His bestehen müßte. Um E+ zu schreiben müßte man C zu His umdeuten (enharmonisch verwechseln) um wieder die Terzschichtung zu erhalten.

Das ist aber nun wirklich eine rein theoretische Sache, über die man sich weiterhin keine Gedanken zu machen braucht. Hörbar ist das sowieso nicht.

Zum Abschluß noch einige Beispiele von Dreiklangsumkehrungen. Versuche diese nachzuvollziehen, bevor Du Dich an die Übungen machst.

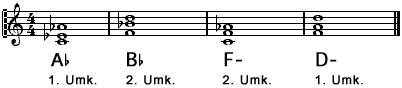
Kleine Eselsbrücke: Steht die obere Note einzeln, ist es die 1. Umkehrung. Stehen die oberen Noten zu zweit, so ist es die zweite Umkehrung.